System Dynamics & Agentenbasierte Modelle

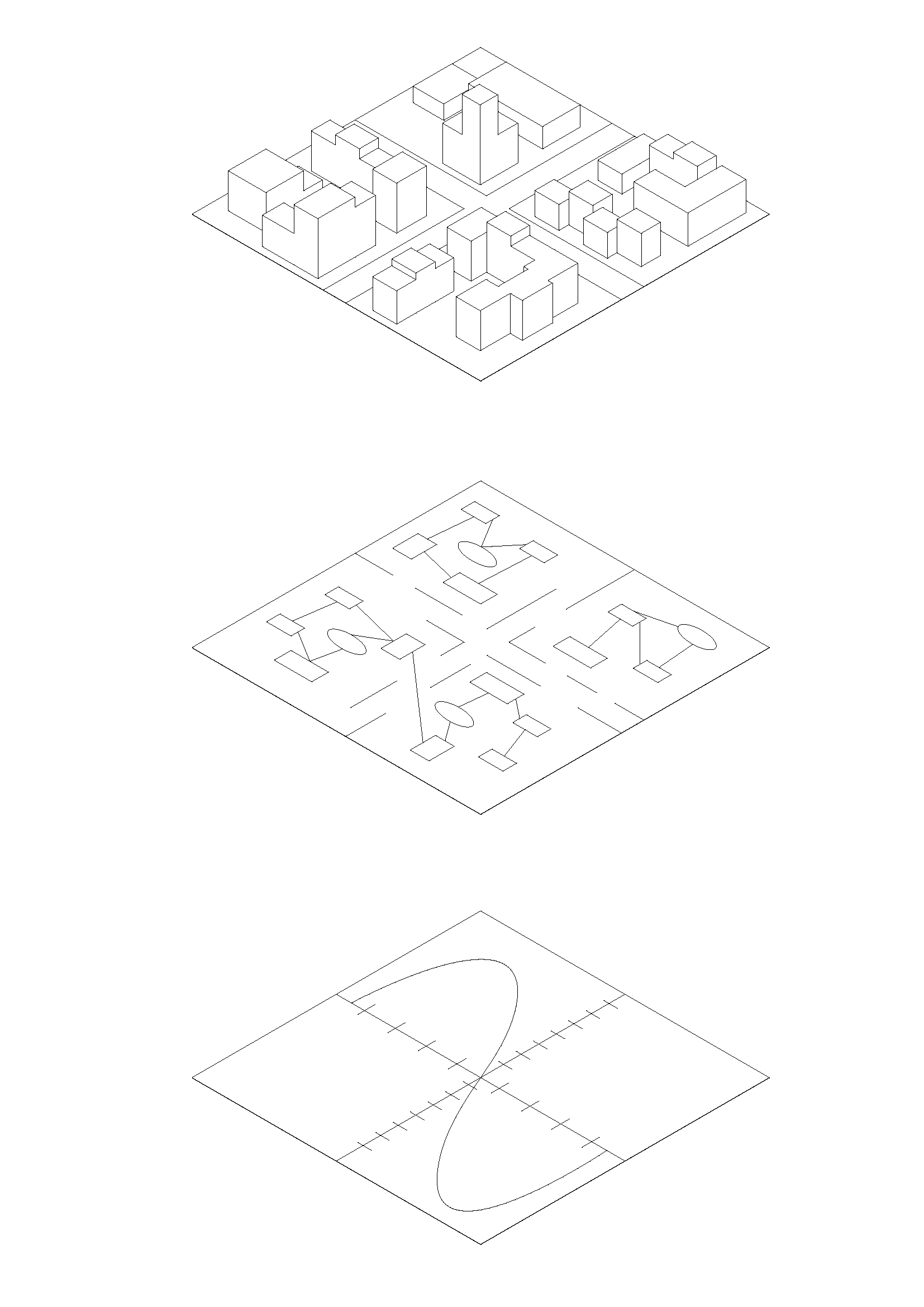
Stadtebene

Städte sind komplexe, adaptive und dynamische Systeme, die eine Vielzahl an Dynamiken mit zahlreichen kausalen Abhängigkeiten beinhalten.

Um die Vielzahl an Subsystemen annähernd abbilden zu können, werden unter anderem System Dynamics Modelle verwendet. System Dynamics ist eine modellbasierte Simulationsmethode basierend auf der allgemeinen Systemtheorie bzw. Kybernetik. Hierbei geht es um die Top-Down-Betrachtung des Verhaltens von komplexen Systemen, die sich durch verzögerte Ursache-Wirkungs-Beziehungen als auch durch Rückkopplungseffekte zwischen einzelnen Variablen auszeichnen. Anstelle der Betrachtung von linearen Ursache-Wirkungsketten werden bei dem System Dynamics Ansatz Kausalitäten eines Systems und ihr Verhalten ganzheitlich und über die Zeit betrachtet. Als zentrale Elemente gelten dabei Feedback-Schleifen, Bestandsgrößen (Stocks) und Flussgrößen (flows). Diese Methode wurde in den 1950er Jahren von Jay W. Forrester entwickelt. Weitere Hintergründe zu System Dynamics findest Du unter anderem hier.

Eine andere Simulationsmethode bilden agentenbasierte Modelle (ABM). Hierbei wird sich dem Verhalten von komplexen Systemen mit einem Bottom-Up-Ansatz angenähert. Auf der betrachteten Stadtebene werden damit einzelne Akteure (im Fachterminus: Agenten) betrachtet, die als eigenständige Entitäten in einem Multi-Agenten Umfeld agieren. Die Interaktionen der Agenten bedingen sich gegenseitig. Durch eine Simulation kann Aufschluss über emergente Phänemäne gewonnen werden. Weitere Hintergründe zu ABM findest Du unter anderem hier

Prozessebene

Blickt man hinter die Fassade der Stadtebene entdeckt man eine Vielzahl an miteinander vernetzten Prozessen. Für bestimmte Fragestellungen und Probleme ist es notwendig, diese Netzwerke zu analysieren, um die Logik von Abläufen zu erkennen, zu verstehen und annähernd abbilden zu können. Wie in der Logik von Prozessdiagrammen setzen sich diese Modelle aus einzelnen Funktionsbausteinen zusammen, dessen Einheit mathematisch berechnet und dadurch simuliert werden kann. Innerhalb eines Modells können diese Bausteine als kleinste betrachtete Einheiten betrachtet werden. Sie simulieren unterschiedliche Zukünfte, also „Was-wäre-wenn…“-Szenarien.

System Dynamics

Bei System Dynamics sind typischerweise Bestände und Flüsse, ergänzt durch Feedbackschleifen und Zeitverzögerungen, die kleinsten Modellierungselemente. Diese Elemente beschreiben kontinuierlich, aggregierte Veränderungen in einem System - bespielsweise die Entwicklung von Bevölkerungszahlen.

Agentenbasierte Modelle

Im Gegensatz dazu bestehen agentenbasierte Modelle aus einer Vielzahl individueller, oft heterogener Agenten als kleinste Einheiten. Die Agenten verfügen über eigene Regeln, Entscheidungslogiken und Verhaltensweisen und interagieren mit ihrer Umwelt sowie miteinander. Das Modellverhalten entsteht hier emergent aus der Mikroebene der Agentenaktionen - also aus dem Zusammenspiel vieler kleiner Einheiten.

Berechnungsebene

System Dynamics

Differenzialgleichungssysteme sind die Berechnungsgrundlage von System Dynamics, da sie zeitabhängige Veränderungen von Zuständen in einem dynamischen System modellieren. Ein Differenzialgleichungssystem besteht aus mehreren gekoppelten Gleichungen, die beschreiben, wie sich Zustandsgrößen über die Zeit verändern.

$\frac{dx_n}{dt} = f_n(x_1, x_2, \ldots, x_n, t)$

Jede Gleichung beschreibt die Änderungsrate einer Zustandsgröße $x_i$ , wie sie sich pro Zeiteinheit verändert in Abhängigkeit von anderen Größen.

• Stocks – Zustandsgrößen $x_n(t)$
• Flows – Änderungsraten $\frac{dx_n}{dt}$
• Feedback loops – Kopplung zwischen Gleichungen (z.B. $f_n$ hängt von $x_n$ ab)
• Simulation – Numerische Lösung dieser Gleichungen über die Zeit

Agentenbasierte Modelle

In agentbasierten Modellen wird statt globalen Gleichungen für das gesamte System das Verhalten einzelner, autonomer Agenten beschrieben, die definierten Regeln folgen, um mit ihrer Umwelt zu interagieren und sich gegenseitig zu beeinflussen. Das globale Systemverhalten ergibt sich aus dem Zusammenspiel vieler individueller Agenten. Agentenbasierte Modelle basieren typischerweise nicht auf Differentialgleichungssystemen, sondern auf regelbasierten Systemen, wie logischen Entscheidungsregeln oder zeitdiskreten Simulationen in aufeinander folgenden Schritten, stochastischen Prozessen wie Übergangswahrscheinlichkeiten zwischen Zuständen, oder der Event-basierten Modellierung der Zustände von einzelnen Agenten. Da die Ergebnisse von der jeweiligen Reihenfolge der Agenteninteraktionen abhängen, können sie nicht deterministisch vorhergesagt werden und erfordern mehrere Simulationsdurchläufe, um ein vollständiges Bild zu erhalten.